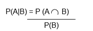Eventos
Primeramente de manera general se presentan los
EVENTOS
- Mutuamente excluyentes: aquellos que no pueden ocurrir al mismo tiempo. EJEMPLO: cara o escudo.
- Independientes: Estos no se ven afectados por otros independientes. EJEMPLO: el color del zapato y la probabilidad que llueva hoy.
- Dependientes: cuando un evento afecta a la probabilidad de ocurrencia de otro. EJEMPLO: repaso, calificaciones.
- No excluyentes entre si: cuando la ocurrencia de uno de ellos no impide que ocurra el otro. EJEMPLO: que una persona sea doctor que tenga 56 años, ser estudiante y ya estar casado.
EVENTOS EXCLUYENTES Y NO EXCLUYENTES. REGLA DE LA ADICIÓN
Eventos mutuamente excluyentes:
Son mutuamente excluyentes o disjuntos si ambos no pueden ser verdaderos (o suceder simultáneamente). Un ejemplo de ello es el resultado de revolear una vez una moneda, el cual solo puede ser "cara" o "cruz", pero no ambos.
Los eventos mutuamente excluyentes son dos resultados de un evento que no pueden ocurrir al mismo tiempo.
- Sacar una carta de un mazo estándar y que salga un as y un rey son eventos mutuamente excluyentes, ya que no pueden ocurrir los dos al mismo tiempo.
- Sin embargo, sacar una carta roja y rey no son eventos mutuamente excluyentes, ya que puedes sacar perfectamente un rey rojo.
Todos los eventos complementarios son mutuamente excluyentes, pero todos los eventos mutuamente excluyentes no son necesariamente complementarios.<>
Los eventos mutuamente excluyentes son aquellos que si un evento sucede significa que el otro no puede ocurrir.
Se les conoce como:
A= Suceso 1 y B= Suceso 2 A y B son excluyentes si la intersección de A y B son cero.
FÓRMULA:
P (A U B) = P(A) + P(B)
Si A y B son eventos mutuamente excluyentes, entonces la probabilidad de que A o B sucedan es equivalente a la probabilidad del evento A más la probabilidad del evento B.
EJEMPLOS:
1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 |
4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 |
5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 |
6,1 | 6,2 | 6,3 | 6,4 | 6,5 | 6,6 |
Se lanzan dos dados simultáneamente, encontrar la probabilidad de obtener la suma de 4 o 6.
P(4) = 3/36 Utilizando la formula
P( 4 U 6 ) = 3/36 + 5/36...
P(6) = 5/36 =8/36

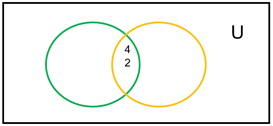
Eventos no mutuamente excluyentes:
Dos o más eventos son no excluyentes, o conjuntos, cuando es posible que ocurran ambos. Esto no indica que necesariamente deban ocurrir estos eventos en forma simultánea.
Son aquellos que a la hora de que suceda no se descarta la posibilidad de otro, es decir puede suceder 2 eventos en el mismo acto.
FORMULA:
P (A U B) = P(A) + P(B) – P (A B)
EJEMPLOS:
Se lanza un dado no cargado. Usted gana $10 si el resultado es menor que 5 o divisible por 2 ¿Cuál es la probabilidad de ganar?
S= espacio muestral S= (1 2 3 4 5 6) A= (1 2 3 4) =4 B= (2 4 6) =3
A= 4/6 B= 3/6
P(A B)= (2 4) =2 P(A B)= 2
Sustituimos la fórmula: 6
4 + 3 - 2 = 5 = 0.83
6 6 6 6
En este video se explican ambos casos...
EVENTOS INDEPENDIENTES:
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo la población donde se obtuvo.
Dos eventos A y B, son independientes si la ocurrencia de uno no tiene que ver con la ocurrencia de otro.
Por definición entonces, A es independiente de B solo la ocurrencia de uno no tiene que ver con la ocurrencia del otro.
Ejemplos los podemos observar en el vídeo para su mayor comprensión:
FORMULA:
P (A intersección B) =P (A) X P (B)
EJEMPLOS:
Se esta realizando una rifa para ganar una guitarra y unas baquetas hay 10 participantes, los ganadores o el ganador se decidirá hasta la 3ra y 4ta vez que se saque el papel. Los primeros 2 papeles sacados se pueden volver a depositar en la urna y seguirán participando, por ende es posible que un solo participante pueda ganar hasta los dos premios. Un participante llamado P compró dos boletos con los números 4 y 9
A: Gane el participante P la guitarra B: Gane el participante P las baquetas
P(A) = 2/10 P(A) X P(B) = 2/10 + 2/10 = 1/25 = 0.04
P(B)= 2/10
EVENTOS DEPENDIENTES:
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió
FORMULA:
P(A intersección B) = P (A) X P (B/A) o P (A intersección B) = P(B) X P(A/B)
3 EVENTOS CONDICIONALES:
La Probabilidad Condicional (o Probabilidad Condicionada) es la probabilidad de que ocurra un suceso A sabiendo que también ocurre otro suceso B.
Formula: